细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。
如图在三角形abc中abac角bac＝120度ad⊥bc于点d
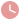
在三角形ABC中,角BAC=120度,以BC为边向形外作等边三角
2013年6月6日 在三角形ABC中,角BAC=120度,以BC为边向形外作等边三角形BCD,把三角形ABD绕着点D按解：∵ BCD是等边三角形 ∴∠BDC=∠BCD=60。 ∵∠BAC=120。 如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，那么∠C=度． ∴∠C=20°． 故答案是：20°． 由AB+BD=DC，易想到可作辅助线DE=DB，然后连接AE，从而可出现两个 如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD 如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，那么∠C= 度． 【答案】 分析： 由AB+BD=DC，易想到可作辅助线DE=DB，然后连接AE，从而可出现两个等腰三角形，一个 如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD 如图,在三角形ABC中,角BAC=120度,以BC为边向外做等边三角形BCD,连接AD,把三角形ABD绕点D按顺时针方向旋转60度后得到三角形ECD，已知AB=3,ac=2求角BAD的度数与AD的长。如图,在三角形ABC中,角BAC=120度,以BC为边向外做等边
如图，在 ABC中，∠BAC=120°，AD⊥BC于点D，且AB
如图，在 ABC中，∠BAC=120°，AD⊥BC于点D，且AB+BD=DC，则∠C的度数是 ( ) A20° B25° C30° D45° 在DC上截取DE=DB， ∵∠ADB=∠ADE=90°，AD=AD， ∴ ADB≌ ADE， （方法二）将 ABD绕点A逆时针旋转120°得到 ACF，取CF的中点G，连接EF、EG，由AB=AC=2$\sqrt{3}$、∠BAC=120°，可得出∠ACB=∠B=30°，根据旋转的性质可得 如图在 ABC中AB=AC=2$\sqrt{3}$∠BAC=120°点DE都在 【答案】分析：由 ABC中，AB=AC，∠BAC=120°，利用等边对等角及三角形的内角和定理求出∠B=∠C=30°，再由AB=AC，且D为BC的中点，利用三线合一得到AD垂直于BC，又DE垂直 如图 ABC中AB=AC∠BAC=120°D是BC的中点DE⊥AB于E 如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，那么∠C=度． 已知,如图,三角形ABC中,AB=AC,D点在BC上,且BD=AD,DC=AC求角B的度数 二维码如图,在三角形ABC中,已知角BAC=120度,AD垂直于BC,AB
如图,在三角形ABC中,AB=AC,角BAC=120度,AB的垂直平分
【题目】如图，在三角形ABC中，AB=AC,∠BAC=120,AB的垂直平分线交BC于点D,交A B于点E,如果DE=1,求BC的长。 【解析】∵∠BAC=120°，AB=AC, ∴∠B=∠C=30°， 在RT BDE 分析：根据三角形内角和定理，由∠BAC=120°，∠B=30°，AD⊥AB求得∠DAC=∠C=30°，由此证得 ADC是等腰三角形，即可求出AD的长，解Rt ABD，得出BD、AB的长，求出BC=BD+CD，再 如图 ABC中∠BAC=120°∠B=30°AD⊥AB垂足为ACD 已知：如图，在三角形ABC中，点 D、E分别在边AB、AC上，且∠ABE=∠ACD，BE、CD交于点G．（1）求证： ABE～ ACD；（2）如果BE平分∠ 已知：如图，在三角形ABC中，点 D、E分别在边AB、AC上 2014年2月19日 如图，在三角形abc中，ab等于ac，角bac等于120度，AD垂直于ac，交BC于点d，求证BC∵∠BAC=120°，AB=AC∴∠B＝∠C＝30°∵AD⊥AC∴ ACD为直角三角形∴DC=2AD （30 °角所对的直角边是斜边的一半）∵∠BAD=∠BAC∠DA 如图，在三角形abc中，ab等于ac，角bac等于120度，AD
如图，在三角形ABC中，角BAC=120度，以BC为边向外做
2011年10月30日 如图，在三角形ABC中，角BAC=120度，以BC为边向外做等边三角形BCD，连接AD，把三角形ABD绕点D按顺时针方向解:由旋转可知： ABD全等于 ECD∴AB=EC=3,∠BAD=∠EAD=ED∵∠ADE=60°∴ ADE是等边三角形∴AE=AD∠E=60°2018年4月19日 在 ABC中，AD⊥BC于点D，∠BAC=45°，BD=3，DC=2，则 ABC的面积为解：如图，把 ABD沿AB为对称轴翻折成为 ABE， ACD沿AC为对称轴翻折成为 ACG，延长EB、GC相交于点F，则 ABE≌ ABD， ACD≌ ACG，所以在 ABC中，AD⊥BC于点D，∠BAC=45°，BD=3，DC=2 2019年8月25日 如图， ABC中，AB=AC，∠BAC=120°，AD⊥AC交BC于点D，求证：BC=3ADAB=AC,∠BAC=120°,即∠C=∠B=30°AD⊥AC交BC于点D,即∠DAC=90°直角三角形中，30度所对的边等于斜边的一半即2AD=DCAD=BD所以BC=3AD如图， ABC中，AB=AC，∠BAC=120°，AD⊥AC交BC于点D 如图，在 ABC中，∠BAC=90°，AD⊥BC于点D，点E为AC的中点，ED的延长线交AB的延长线于点F．求证： ，然后利用等量代换得到结论．本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中 如图，在 ABC中，∠BAC=90°，AD⊥BC于点D，点E为AC的
(2020重庆A卷)如图,在Rt ABC中,∠BAC=90°,AB=AC,点D是
(2020重庆A卷)如图,在Rt ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,D ABC为等边三角形,AB=8,AD⊥BC于点D,E为线段AD上一点,AE=以AE为边在直线AD右侧构造等边三角形AEF,连接CE,N为CE的 如图，在 ABC中，AC>AB，AD平分∠BAC，点D到点B与点C的距离相等，过点D作DE⊥BC于点A．(1)求证：BE＝CE；(2)请直接写出∠ABC，∠ACB，∠ADE三者之间的数量关系；(3)若∠ACB＝40°，∠ADE＝20°，求∠DCB的度数．B DA E如图,在 ABC中,AC>AB,AD平分∠BAC,点D到点B与点C的 2012年6月23日 在三角形ABC中，角BAC=120度，AD垂直BC于点D，且AB+BD=DC,求角C的度数在DC上截取一段DE，使DE=DB 用边角边证的三角形ABD全等于三角形ACD 所以 AB=AC 角AEB=角B 又因为 AB+BD=DC在三角形ABC中，角BAC=120度，AD垂直BC于点D，且AB 如图在三角形ABC中角bac等于90度,AB等于AC,点d是AB的中点,连接CD,过点b作be垂直于CD交CD的有延长线于点e,连接AE,过点A作AF垂直于CD于点f (1)求证AE等于AF（2）求证CD=2be+de如图,在三角形ABC中,角BAC等于90度 AB等于AC,D是AC上
【题目】如图,在等腰三角形ABC中,AB=AC,∠BAC=120°, AD
【解析】(1)连接BO,如图1所示:PABBC图1AB=AC,AD⊥BC∴BD=CD,∠ODB=∠ODC在 OBD和 OCD中OD= OD ∠ODB=∠ODCBD= OBD= OCD(SAS)OB=OC,又OP=OC∴OB=OC=OP∴∠APO=∠ABO,∠DBO=∠DCO又∠BAC=120°∠ABC=∠ACB=30°,又∠ABD=∠ 如图,在三角形ABC中,AB=AC,角BAC=120度,AB的垂直平分线交BC于点D,交AB于点E,如果DE=1,求BC的长 百度试题 结果1 结果2 结果3 题目 如图,在三角形ABC中,AB=AC,角BAC=120度,AB的垂直平分线交BC于点D,交AB于点E,如果DE=1,求BC的长 相关知识 如图,在三角形ABC中,AB=AC,角BAC=120度,AB的垂直平分 为帮助你解决这道题,我将一步步引导你如何攻克它注意学习解决问题的方法1先在草稿纸上画一遍图,对所给条件有个简单印象2从问题入手,题目证 AB垂直平分DF3想象一下垂直平分相关的,再结合图,你便知道假如我证明到三角形BDF是等腰直角三角形而BG是1如图所示,在Rt三角形ABC中,角ACB=90度,AC=BC,D为BC （1）证明：如图，连接CD，交AB于点F，AD=BD点C和点D均在线段AB的垂直平分线上直线CD为线段AB的垂直平分线为等腰直角三角形(2)如（1）中图所示若，则线段AE的长为1(1)连接CD，交AB于点F，则由线段垂直平分线的判定定理可得，直线CD是线段AB的 如图所示，在三角形ABC中，角ABC＝90度，AC=BC,D为
【题文】如图，在等腰三角形ABC中，AB=AC，∠BAC=120
如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;② OPC是等边三角形;③AC=AO+AP;④S ABC=S四边形AOCP其中所有正确结论的序号为( ) A ①②③ B 2015年1月20日 如图，∠BAC=45°，AD⊥BC于点D，且BD=3，CD=2，则AD的长为如图，过B作BE⊥AC，垂足为E交AD于F∵∠BAC=45°∴BE=AE，∵∠C+∠EBC=90°，∠C+∠EAF=90°，∴∠EAF=∠EBC，在 AFE与 如图，∠BAC=45°，AD⊥BC于点D，且BD=3，CD=2，则AD 如图，已知等腰 ABC中，AB=AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，(1)求∠APO+∠DCO的度数; (2)求证:点P在OC的垂直平分线上如图，已知等腰 ABC 2012年11月11日 如图，在三角形ABC中，AB=AC，角BAC=120度，AD垂直AC交BC于点D求证：BC=3AD∵∠BAC=120°，AB=AC∴∠B＝∠C＝30°∵AD⊥AC∴ ACD为直角三角形∴DC=2AD （30°角所对的直角边是斜边的一半）∵∠BAD=∠BAC∠DAC=12 百度首页 如图，在三角形ABC中，AB=AC，角BAC=120度，AD垂直
如图，在等腰直角三角形ABC
如图，在等腰直角三角形ABC中，AB=AC，∠BAC=90°，BF平分∠ABC，CD⊥BD交BF的延长线于点 D试说明BF=2C D 解:延长BA,CD交于点E∵BF平分∠ABC,CD⊥BD,BD=BD,∴ BDC≌ BDE,∴BC=BE 2017年9月2日 如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，OP与AC相交与点M，则下列结论：①点O是 PBC的外心；② MAO∽ MPC；③AC=AO+AP；④S ABC=45S四边形AOCP．其中正确的如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D 如图所示,在三角形ABC中,角BAC=90度,AD垂直于BC于D 百度试题 结果1 结果2 结果3 题目 如图所示,在三角形ABC中,角BAC=90度,AD垂直于BC于D 如图所示,在三角形ABC中,角BAC=90度,AD垂直于BC于D 问题情境：如图①,在直角三角形ABC中,∠BAC=90∘,AD⊥BC于点D,可知：∠BAD=∠C(不需要证明)；(1)特例探究：如图②,∠MAN=90∘,射线AE在这个角的内部,点 BC在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点 D证明： ABD≌ CAF；(2)归纳 (10分)问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD
在三角形ABC中，角BAC等于120度，AD垂直于BC于点D
2011年11月13日 在三角形ABC中，角BAC等于120度，AD垂直于BC于点D，且AB+BD等于DC,求角C的度数在DC上截取一段DE，使DE=DB 用边角边证的三角形ABD全等于三角形ACD 所以 AB=AC 角AEB=角B 又因为 AB+BD=DC如图, ABC的∠BAC=120°,AB=3,AC=2,以BC为边向外作等边 BCD,把 ABD绕着D点按顺时针方向旋转60°后到 ECD的位置（1）求∠DAE的度数（2）求AD的长如图,在三角形ABC中,角BAC=120度,以BC为边向外做等边 2024年6月27日 如图，在 ABC中，AB=AC，∠BAC=120°．D是AB边上一点，DE⊥AC交CA的延长线于点E．（1）用等式表示AD与AE的数量关系，并证明；（2）连接B 菁于教，优于学 旗下产品 校本题库 菁优备课 开放平台 菁优测评 菁优公式 小优同学 菁优App 数字备考 如图，在 ABC中，AB=AC，∠BAC=120°．D是AB边上一点 2015年1月14日 如图，已知等腰三角形ABC中，AB=AC，∠BAC=120º，AD⊥BC于点D，点P是BA 延长线上首先，我先把相应的图给你发上。题：第二题：第三题：第四题：希望能帮到你 百度首页 商城 注册 登录 资讯 视频 图片 知道 如图，已知等腰三角形ABC中，AB=AC，∠BAC=120º，AD
如图1，在RT三角形ABC中，角BAC=90，AD垂直BC于点D
2011年9月3日 如图1，在RT三角形ABC中，角BAC=90，AD垂直BC于点D，点O是AC边上一点，连接BO交AD于F，OE垂直OB交BC边2016年10月27日 如图，在三角形abc中，角bac等于90度，ad垂直bc于d，be平分角abc交ad于点f，1、等腰 AEF证明：∵∠BAC＝90∴∠ABC+∠C＝90∵AD⊥BC∴∠ABC+∠BAD＝90∴∠BAD＝∠C∵BE平分∠ABC∴∠ABE＝∠CBE∵∠AEF＝∠BAD+∠ABE,如图，在三角形abc中，角bac等于90度，ad垂直bc于d，be E AD BC如图，在 ABC中，AB=AC，∠BAC=120°，点D为AB边上一点（不与点B重合），连接CD，将线段CD绕点D逆时针旋转90°，点C的对应点为E，连接BE．若AB=2，则 BDE面积的最大值为．如图，在 ABC中，AB=AC，∠BAC=120°，点D为AB边上 45°[分析]延长CH交AB于点F,利用三角形的三条高交于一点可得CF⊥AB,利用三角形的内角和定理即可分别求出∠ABC、∠BCF和∠CHD[详解]解:延长CH交AB于点F∵在ABC中,三边的高交于一点,∴CF⊥AB,A E E H B D C∵∠ACB=60°,∠BAC=75°,∴∠ABC=180°∠如图，在 ABC中，∠ACB=60°，∠BAC=75°，AD⊥BC于点D
在三角形ABC中,角BAC=120度,以BC为边向形外作等边三角
2013年6月6日 在三角形ABC中,角BAC=120度,以BC为边向形外作等边三角形BCD,把三角形ABD绕着点D按解：∵ BCD是等边三角形 ∴∠BDC=∠BCD=60。 ∵∠BAC=120。 ∴∠ABD+∠ACD=180 。如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，那么∠C=度． ∴∠C=20°． 故答案是：20°． 由AB+BD=DC，易想到可作辅助线DE=DB，然后连接AE，从而可出现两个等腰三角形，一个是 ABE，一个是 ACE，利用三角形外角的性质，易求∠B=2∠C，再利用三角形内角和定理可求∠C． 本题考点：等腰三角形的性质． 考点点评：本题考查了线段垂直平分线的判 如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD 2014年11月9日 如图， ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）A．20°B．25°C．30°D．大解：如图，在DC上取DE=DB．连接AE，在Rt ABD和Rt AED中，BD=ED，AD=AD．∴ ABD≌ AED．∴AB=AE，∠B=∠AE如图， ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，那么∠C= 度． 【答案】 分析： 由AB+BD=DC，易想到可作辅助线DE=DB，然后连接AE，从而可出现两个等腰三角形，一个是 ABE，一个是 ACE，利用三角形外角的性质，易求∠B=2∠C，再利用三角形内角和定理可求∠C． 如图，在 ABC中，∠BAC＝120°，AD⊥BC于D，且AB+BD＝DC，求∠C的度数．如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD
如图,在三角形ABC中,角BAC=120度,以BC为边向外做等边
如图,在三角形ABC中,角BAC=120度,以BC为边向外做等边三角形BCD,连接AD,把三角形ABD绕点D按顺时针方向旋转60度后得到三角形ECD，已知AB=3,ac=2求角BAD的度数与AD的长。2018年3月21日 如图,三角形ABC中,角BAC=120度,AD垂直BC于D,且AB+BD=DC,求角C的度数 （用两种方法）方法1：延长DB至E使得BE=BA，则DE=DB+BE=DB+BA=DC，易证ADE全等于ADC，AC=AE，所以三角形ACE为等腰三角形，角AEB=角C又，角ABC=角A如图,三角形ABC中,角BAC=120度,AD垂直BC于D,且AB+BD=DC,求角如图，在 ABC中，∠BAC=120°，AD⊥BC于点D，且AB+BD=DC，则∠C的度数是 ( ) A20° B25° C30° D45° 在DC上截取DE=DB， ∵∠ADB=∠ADE=90°，AD=AD， ∴ ADB≌ ADE， ∴∠B=∠AED，AB=AE， ∵AB+BD=DC，∴AE+DE=DC， ∵DE+EC=DC，∴AE=EC， ∴∠EAC=∠C， ∴∠B=∠AED=2∠C， ∵∠BAC=120°， ∴∠B+∠C=3∠C=60°， ∴∠C=20°， 故选A 故答案为：a如图，在 ABC中，∠BAC=120°，AD⊥BC于点D，且AB （方法二）将 ABD绕点A逆时针旋转120°得到 ACF，取CF的中点G，连接EF、EG，由AB=AC=2$\sqrt{3}$、∠BAC=120°，可得出∠ACB=∠B=30°，根据旋转的性质可得出∠ECG=60°，结合CF=BD=2CE可得出 CEG为等边三角形，进而得出 CEF为直角三角如图在 ABC中AB=AC=2$\sqrt{3}$∠BAC=120°点DE都在
如图 ABC中AB=AC∠BAC=120°D是BC的中点DE⊥AB于E
【答案】分析：由 ABC中，AB=AC，∠BAC=120°，利用等边对等角及三角形的内角和定理求出∠B=∠C=30°，再由AB=AC，且D为BC的中点，利用三线合一得到AD垂直于BC，又DE垂直于AB，利用同角的余角相等得到∠B=∠EDA=30°，在直角三角形AED中如图，在 ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，那么∠C=度． 已知,如图,三角形ABC中,AB=AC,D点在BC上,且BD=AD,DC=AC求角B的度数 二维码如图,在三角形ABC中,已知角BAC=120度,AD垂直于BC,AB
钾石灰石的先进加工设备
--勘查开膨润土材办证
--磨面的时磨磨面的时磨磨面的时磨
--物料的粉碎
--天津院矿粉磨天津院矿粉磨天津院矿粉磨
--刷腻子多少钱
--欧版雷蒙磨的白云石板是什么形状的
--ZG石灰石X重钙磨粉机雷蒙机
--生石灰的加工设备
--白云石工业磨粉机结构图
--吉林市方解石立磨生产线投资多少
--黑龙江齐齐哈尔石灰石制粉生产线
--氧化铁雾化设备价格
--成都微粉磨设备
--碳酸钙筛规格
--珍珍岩矿石磨粉机
--旗舰高速多功能粉碎机,
--方大炭素收购中钢吉炭
--稀土矿粉磨程序
--石屑pc401290石灰石碳酸钙磨粉机
--砖厂煅烧窑煤粉制备系统
--上海稀土采矿机
--世邦粉碎雷蒙机
--上海黎明矿石磨粉机制造
--粉碎去籽机器
--福建泉州雷蒙磨
--微粉磨产品型号及价格
--防爆石一方是几吨
--ncf1416石膏石矿石磨粉机
--仪器仪表矿石磨粉机粉碎机
--